728x90
오늘은 재귀에 대해서 알아보자.
재귀(Recursion) 란
사전적 의미 : 본디의 곳으로 다시 돌아오는 것.
즉, 재귀함수란 함수내에서 자기 자신을 호출하는 함수를 의미한다.
[데이터 구조] 재귀
재귀란 ?
medium.com
재귀 함수를 호출하면 재귀 탈출 조건이 없다면 무한반복으로 함수를 호출한다.
예시)
#include <stdio.h>
void Recusive(int num){
if(num <= 0){ // 재귀 탈출 조건
return;
}
printf("Recursive call! %d \n",num);
Recusive(num - 1);
}
int main(void){
Recusive(3);
// Recursive call! 3
// Recursive call! 2
// Recursive call! 1
return 0;
}
재귀와 반복 비교
재귀
- 기본 경우에 도달하면 종료한다.
- 각 재귀 호출은 스택 프레임(즉, 메모리) 에 부가 공간을 필요로 한다.
- 무한 재귀에 들어가게 되면 메모리 용량을 초과해서 스택 오버플로우를 초래하게 된다.
- 어떤 문제들의 해답은 재귀적인 수식으로 만들기 쉽다. (다이나믹 프로그래밍 == DP)
반복
- 조건이 거짓일 때 종료한다.
- 각 반복이 부가 공간을 필요로 하지 않는다.
- 무한 루프는 추가 메모리가 필요하지 않으므로 무한히 반복된다.
- 반복적 해법은 재귀적 해법에 비해 간단하지 않을 때가 있다.
재귀 알고리즘의 예시
- 피보나치 수열, 팩토리얼 구하기
- 병합 정렬, 퀵 정렬
- 이진 검색
- 트리 탐색, 중위, 전위, 후위 등 여러 트리 문제들
- 그래프 탐색, 깊이 우선 탐색과 너비 우선 탐색
- 동적 계획법의 예
- 분할 정복 알고리즘
- 하노이의 탑
- 백트래킹 알고리즘
재귀 알고리즘의 예시 코드
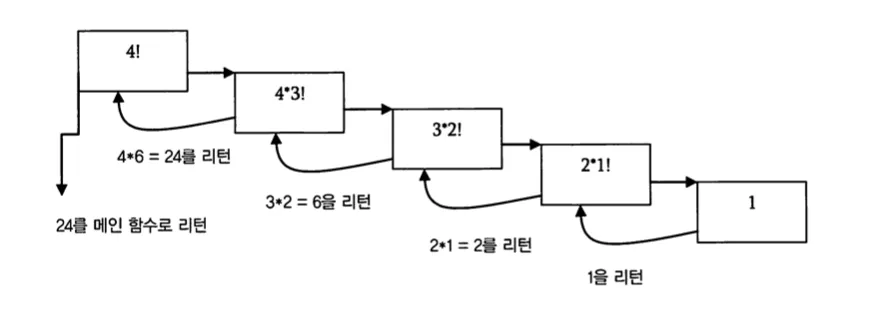
팩토리얼 함수
#include <stdio.h>
int Factorial(int n){
if(n == 0){
return 1;
} else{
return n * Factorial(n-1);
}
}
int main(void){
printf("1! = %d \n",Factorial(1));
printf("2! = %d \n",Factorial(2));
printf("3! = %d \n",Factorial(3));
printf("4! = %d \n",Factorial(4));
printf("9! = %d \n",Factorial(9));
return 0;
}
피보나치 수열
#include<stdio.h>
int Fibo(int n){
if(n == 1){
return 0;
}
else if(n == 2){
return 1;
}
else return Fibo(n - 1) + Fibo(n - 2);
}
int main(void){
int i;
for(int i=1; i<15; i++){
printf("%d ",Fibo(i));
}
return 0;
}
이진 탐색
#include<stdio.h>
int BSearchRecur(int arr[], int first, int last, int target){
int mid;
if(first > last) return -1;
mid = (first + last) / 2;
if(arr[mid] == target) return mid;
else if(target < arr[mid]) return BSearchRecur(arr, first, mid - 1, target);
else return BSearchRecur(arr, mid+1, last, target);
}
int main(void){
int arr[] = {1,3,5,7,9};
int idx;
idx = BSearchRecur(arr, 0, sizeof(arr)/sizeof(int) -1 , 7);
if(idx == -1){
printf("탐색 실패\n");
} else{
printf("탐색 저장 인덱스: %d",idx);
}
return 0;
}
하노이 타워
#include<stdio.h>
void HanoiTowerMove(int num, char from, char by, char to){
if(num == 1){
printf("원반 1에서 %c에서 %c로 이동\n", from,to);
}
else{
HanoiTowerMove(num - 1, from, to, by);
printf("원반%d을(를) %c에서 %c로 이동\n",num,from,to);
HanoiTowerMove(num - 1, by, from, to );
}
}
int main(void){
HanoiTowerMove(3,'A','B','C');
return 0;
}
참고
[데이터 구조] 재귀
재귀란 ?
medium.com
열혈 자료구조
728x90
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 동적 계획법(Dynamic Programming) (0) | 2023.07.30 |
|---|---|
| [Algorithm] 배낭 문제(knapsack) 냅색 알고리즘 (0) | 2023.07.27 |
| [Algorithm] 0-1 BFS (0) | 2023.07.01 |
| [Algorithm] 내가 지금 현재 풀고 있는 알고리즘 사이트 (0) | 2023.05.04 |
| [Algorithm] DFS와 BFS (0) | 2023.05.03 |
728x90
오늘은 재귀에 대해서 알아보자.
재귀(Recursion) 란
사전적 의미 : 본디의 곳으로 다시 돌아오는 것.
즉, 재귀함수란 함수내에서 자기 자신을 호출하는 함수를 의미한다.

[데이터 구조] 재귀
재귀란 ?
medium.com
재귀 함수를 호출하면 재귀 탈출 조건이 없다면 무한반복으로 함수를 호출한다.
예시)
#include <stdio.h>
void Recusive(int num){
if(num <= 0){ // 재귀 탈출 조건
return;
}
printf("Recursive call! %d \n",num);
Recusive(num - 1);
}
int main(void){
Recusive(3);
// Recursive call! 3
// Recursive call! 2
// Recursive call! 1
return 0;
}
재귀와 반복 비교
재귀
- 기본 경우에 도달하면 종료한다.
- 각 재귀 호출은 스택 프레임(즉, 메모리) 에 부가 공간을 필요로 한다.
- 무한 재귀에 들어가게 되면 메모리 용량을 초과해서 스택 오버플로우를 초래하게 된다.
- 어떤 문제들의 해답은 재귀적인 수식으로 만들기 쉽다. (다이나믹 프로그래밍 == DP)
반복
- 조건이 거짓일 때 종료한다.
- 각 반복이 부가 공간을 필요로 하지 않는다.
- 무한 루프는 추가 메모리가 필요하지 않으므로 무한히 반복된다.
- 반복적 해법은 재귀적 해법에 비해 간단하지 않을 때가 있다.
재귀 알고리즘의 예시
- 피보나치 수열, 팩토리얼 구하기
- 병합 정렬, 퀵 정렬
- 이진 검색
- 트리 탐색, 중위, 전위, 후위 등 여러 트리 문제들
- 그래프 탐색, 깊이 우선 탐색과 너비 우선 탐색
- 동적 계획법의 예
- 분할 정복 알고리즘
- 하노이의 탑
- 백트래킹 알고리즘
재귀 알고리즘의 예시 코드
팩토리얼 함수
#include <stdio.h>
int Factorial(int n){
if(n == 0){
return 1;
} else{
return n * Factorial(n-1);
}
}
int main(void){
printf("1! = %d \n",Factorial(1));
printf("2! = %d \n",Factorial(2));
printf("3! = %d \n",Factorial(3));
printf("4! = %d \n",Factorial(4));
printf("9! = %d \n",Factorial(9));
return 0;
}
피보나치 수열
#include<stdio.h>
int Fibo(int n){
if(n == 1){
return 0;
}
else if(n == 2){
return 1;
}
else return Fibo(n - 1) + Fibo(n - 2);
}
int main(void){
int i;
for(int i=1; i<15; i++){
printf("%d ",Fibo(i));
}
return 0;
}
이진 탐색
#include<stdio.h>
int BSearchRecur(int arr[], int first, int last, int target){
int mid;
if(first > last) return -1;
mid = (first + last) / 2;
if(arr[mid] == target) return mid;
else if(target < arr[mid]) return BSearchRecur(arr, first, mid - 1, target);
else return BSearchRecur(arr, mid+1, last, target);
}
int main(void){
int arr[] = {1,3,5,7,9};
int idx;
idx = BSearchRecur(arr, 0, sizeof(arr)/sizeof(int) -1 , 7);
if(idx == -1){
printf("탐색 실패\n");
} else{
printf("탐색 저장 인덱스: %d",idx);
}
return 0;
}
하노이 타워
#include<stdio.h>
void HanoiTowerMove(int num, char from, char by, char to){
if(num == 1){
printf("원반 1에서 %c에서 %c로 이동\n", from,to);
}
else{
HanoiTowerMove(num - 1, from, to, by);
printf("원반%d을(를) %c에서 %c로 이동\n",num,from,to);
HanoiTowerMove(num - 1, by, from, to );
}
}
int main(void){
HanoiTowerMove(3,'A','B','C');
return 0;
}
참고
[데이터 구조] 재귀
재귀란 ?
medium.com
열혈 자료구조
728x90
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 동적 계획법(Dynamic Programming) (0) | 2023.07.30 |
|---|---|
| [Algorithm] 배낭 문제(knapsack) 냅색 알고리즘 (0) | 2023.07.27 |
| [Algorithm] 0-1 BFS (0) | 2023.07.01 |
| [Algorithm] 내가 지금 현재 풀고 있는 알고리즘 사이트 (0) | 2023.05.04 |
| [Algorithm] DFS와 BFS (0) | 2023.05.03 |
