DFS와 BFS 란
DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)는 그래프 탐색 알고리즘입니다. 이 두 알고리즘은 그래프의 노드를 탐색하는 방식에서 차이가 있습니다.
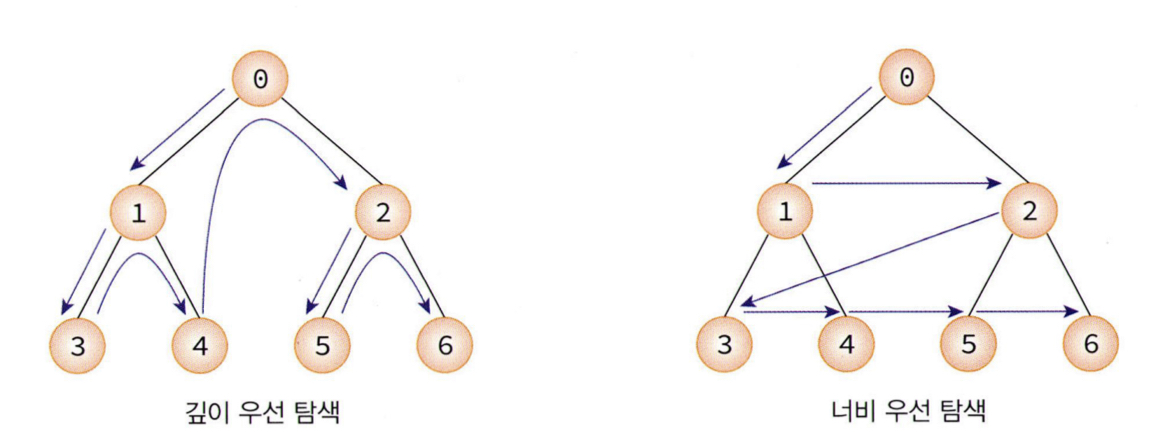
DFS는 한 노드에서 시작하여 깊이를 우선으로 탐색하며, 해당 경로가 더 이상 진행할 수 없을 때 되돌아가서 다른 경로를 탐색합니다. 스택이나 재귀 함수를 사용하여 구현할 수 있습니다. DFS는 그래프의 깊은 부분을 우선적으로 탐색하므로, 해답이 깊은 단계에 위치한 경우 효율적일 수 있습니다. 하지만 무한 루프에 빠질 수 있으며, 최단 경로를 찾는 문제에서는 최적의 해를 보장하지 않을 수 있습니다.
BFS는 한 노드에서 시작하여 인접한 모든 노드를 먼저 탐색한 후, 그 다음 레벨의 인접한 노드를 탐색합니다. 큐를 사용하여 구현할 수 있습니다. BFS는 그래프의 넓은 영역을 우선적으로 탐색하므로, 최단 경로를 찾는 문제에서 보다 효율적입니다. 또한, 무한 그래프에서도 유한한 시간 내에 탐색을 완료할 수 있습니다. 하지만 그래프의 깊은 부분을 우선적으로 탐색하지 않기 때문에, DFS보다 더 많은 메모리를 필요로 할 수 있습니다.
DFS
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
class Graph {
private int vertices;
private List<List<Integer>> adjacencyList;
public Graph(int vertices) {
this.vertices = vertices;
adjacencyList = new ArrayList<>(vertices);
for (int i = 0; i < vertices; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public void addEdge(int source, int destination) {
adjacencyList.get(source).add(destination);
}
public void DFS(int startVertex) {
boolean[] visited = new boolean[vertices];
Stack<Integer> stack = new Stack<>();
visited[startVertex] = true;
stack.push(startVertex);
while (!stack.isEmpty()) {
int currentVertex = stack.pop();
System.out.print(currentVertex + " ");
List<Integer> neighbors = adjacencyList.get(currentVertex);
for (int neighbor : neighbors) {
if (!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
}
}
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph(6);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
graph.addEdge(3, 5);
System.out.println("DFS traversal starting from vertex 0:");
graph.DFS(0);
}
}
BFS
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
class Graph {
private int vertices;
private List<List<Integer>> adjacencyList;
public Graph(int vertices) {
this.vertices = vertices;
adjacencyList = new ArrayList<>(vertices);
for (int i = 0; i < vertices; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public void addEdge(int source, int destination) {
adjacencyList.get(source).add(destination);
}
public void BFS(int startVertex) {
boolean[] visited = new boolean[vertices];
Queue<Integer> queue = new LinkedList<>();
visited[startVertex] = true;
queue.offer(startVertex);
while (!queue.isEmpty()) {
int currentVertex = queue.poll();
System.out.print(currentVertex + " ");
List<Integer> neighbors = adjacencyList.get(currentVertex);
for (int neighbor : neighbors) {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.offer(neighbor);
}
}
}
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph(6);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
graph.addEdge(3, 5);
System.out.println("BFS traversal starting from vertex 0:");
graph.BFS(0);
}
}위의 코드들은 DFS와 BFS를 인접 리스트로 구현한 예시입니다.
그래프의 정점 수를 vertices로 설정하고, addEdge 메서드로 간선을 추가합니다.
DFS 및 BFS 메서드를 사용해서 시작 정점으로부터 DFS와 BFS를 실행하여 순회한 결과를 출력합니다.
DFS : 0 2 4 1 3 5
BFS : 0 1 2 3 4 5
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 0-1 BFS (0) | 2023.07.01 |
|---|---|
| [Algorithm] 내가 지금 현재 풀고 있는 알고리즘 사이트 (0) | 2023.05.04 |
| [Algorithm] 유니온 파인드(Union-Find) 알고리즘 (0) | 2023.04.21 |
| [Algorithm] 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2023.04.14 |
| [Algorithm] 그리디 알고리즘 (Greedy) (2) | 2023.04.06 |
DFS와 BFS 란
DFS(깊이 우선 탐색)와 BFS(너비 우선 탐색)는 그래프 탐색 알고리즘입니다. 이 두 알고리즘은 그래프의 노드를 탐색하는 방식에서 차이가 있습니다.
DFS는 한 노드에서 시작하여 깊이를 우선으로 탐색하며, 해당 경로가 더 이상 진행할 수 없을 때 되돌아가서 다른 경로를 탐색합니다. 스택이나 재귀 함수를 사용하여 구현할 수 있습니다. DFS는 그래프의 깊은 부분을 우선적으로 탐색하므로, 해답이 깊은 단계에 위치한 경우 효율적일 수 있습니다. 하지만 무한 루프에 빠질 수 있으며, 최단 경로를 찾는 문제에서는 최적의 해를 보장하지 않을 수 있습니다.
BFS는 한 노드에서 시작하여 인접한 모든 노드를 먼저 탐색한 후, 그 다음 레벨의 인접한 노드를 탐색합니다. 큐를 사용하여 구현할 수 있습니다. BFS는 그래프의 넓은 영역을 우선적으로 탐색하므로, 최단 경로를 찾는 문제에서 보다 효율적입니다. 또한, 무한 그래프에서도 유한한 시간 내에 탐색을 완료할 수 있습니다. 하지만 그래프의 깊은 부분을 우선적으로 탐색하지 않기 때문에, DFS보다 더 많은 메모리를 필요로 할 수 있습니다.

DFS
import java.util.ArrayList;
import java.util.List;
import java.util.Stack;
class Graph {
private int vertices;
private List<List<Integer>> adjacencyList;
public Graph(int vertices) {
this.vertices = vertices;
adjacencyList = new ArrayList<>(vertices);
for (int i = 0; i < vertices; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public void addEdge(int source, int destination) {
adjacencyList.get(source).add(destination);
}
public void DFS(int startVertex) {
boolean[] visited = new boolean[vertices];
Stack<Integer> stack = new Stack<>();
visited[startVertex] = true;
stack.push(startVertex);
while (!stack.isEmpty()) {
int currentVertex = stack.pop();
System.out.print(currentVertex + " ");
List<Integer> neighbors = adjacencyList.get(currentVertex);
for (int neighbor : neighbors) {
if (!visited[neighbor]) {
visited[neighbor] = true;
stack.push(neighbor);
}
}
}
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph(6);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
graph.addEdge(3, 5);
System.out.println("DFS traversal starting from vertex 0:");
graph.DFS(0);
}
}
BFS
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
class Graph {
private int vertices;
private List<List<Integer>> adjacencyList;
public Graph(int vertices) {
this.vertices = vertices;
adjacencyList = new ArrayList<>(vertices);
for (int i = 0; i < vertices; i++) {
adjacencyList.add(new ArrayList<>());
}
}
public void addEdge(int source, int destination) {
adjacencyList.get(source).add(destination);
}
public void BFS(int startVertex) {
boolean[] visited = new boolean[vertices];
Queue<Integer> queue = new LinkedList<>();
visited[startVertex] = true;
queue.offer(startVertex);
while (!queue.isEmpty()) {
int currentVertex = queue.poll();
System.out.print(currentVertex + " ");
List<Integer> neighbors = adjacencyList.get(currentVertex);
for (int neighbor : neighbors) {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.offer(neighbor);
}
}
}
}
}
public class Main {
public static void main(String[] args) {
Graph graph = new Graph(6);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 4);
graph.addEdge(3, 5);
System.out.println("BFS traversal starting from vertex 0:");
graph.BFS(0);
}
}위의 코드들은 DFS와 BFS를 인접 리스트로 구현한 예시입니다.
그래프의 정점 수를 vertices로 설정하고, addEdge 메서드로 간선을 추가합니다.
DFS 및 BFS 메서드를 사용해서 시작 정점으로부터 DFS와 BFS를 실행하여 순회한 결과를 출력합니다.
DFS : 0 2 4 1 3 5
BFS : 0 1 2 3 4 5
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 0-1 BFS (0) | 2023.07.01 |
|---|---|
| [Algorithm] 내가 지금 현재 풀고 있는 알고리즘 사이트 (0) | 2023.05.04 |
| [Algorithm] 유니온 파인드(Union-Find) 알고리즘 (0) | 2023.04.21 |
| [Algorithm] 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2023.04.14 |
| [Algorithm] 그리디 알고리즘 (Greedy) (2) | 2023.04.06 |
