배낭 문제(knapsack) 냅색 알고리즘이란
Knapsack Problem, 배낭문제는 다이나믹 프로그래밍에서 매우 유명한 문제이다.
조합 최적화(Combination Optimization) 문제 중 하나로, 주어진 공간(배낭)에 최대 가치를 가지는 물건들을 선택하는 문제이다.
일반적으로 배낭에 넣을 수 있는 총 무게(용량)가 주어지고, 물건의 무게와 해당 물건을 배낭에 넣을 때의 가치가 주어진다.
배낭 문제에는 크게 2가지의 유형이 있다.
0/1 배낭 문제(0/1 Knapscak Problem)
이 유형에서는 각 물건을 배낭에 넣을지(1) 또는 넣지 않을지(0)를 결정해야한다. 즉, 각 물건은 배낭에 한 번만 들어갈 수 있다. 이러한 제약 때문에 0/1 이라는 이름이 붙었다. 이 유형의 배낭 문제는 NP-hard문제로 알려져 있으며, 모든 가능한 조합을 시도해보려는 브루트포스(Brute-force) 방법으로는 효율적으로 해결 할 수 가 없다. 즉, DP를 사용해야한다.
분수 배낭 문제(Fractional Knapsack Problem)
이 유형에서는 각 물건을 잘게 쪼개서 일부분만 배낭에 넣을 수 있다. 즉, 물건을 부분적으로 선택할 수 있다. 이 경우 그리디(Greedy) 알고리즘이 사용될 수 있으며, 단위 무게당 가치가 높은 물건부터 차례로 넣는 방식이 최적해를 찾을 수 있다.
알고리즘 별로 유형 정리
Brute Force Approach
만약 n개의 물건이 있을 때, 가능한 모든 조합을 만들기 위해서는 2n 개의 경우의 수를 모두 시도해 보아야한다. 가지고 있는 물건이 몇개 없다면 별로 시간이 오래걸리지는 않겠지만, 2n 은 물건의 갯수가 하나만 늘어도 경우의 수가 크게 늘어나게 된다. 이 연산을 수행하려면 𝛩(2n ) 의 시간을 사용해야하고, 프로그래머 입장에서 그다지 좋은 접근은 아닐 것이다.
Dynamic Programming
따라서 이 문제는 당연스럽게도 다이나믹 프로그래밍으로 해결해야 한다. 그런데 항상 그렇듯 DP 의 가장 큰 어려움은 점화식으로 생각해야한다.
위 접근이 아닌 다른 방법으로 어떻게 접근해야 할까. 배낭에 물건을 넣을 때, 우리가 선택할 수 있는 경우는 두 가지가 있다.
- 물건을 넣는다.
- 물건을 넣지 않는다.
만약 현재 내가 넣으려고 하는 물건의 무게가 전체 제한무게를 초과한다면, 선택지는 물건을 넣지 않는 것 밖에 없다. 따라서 다음과 같은 식을 일단 하나 만들 수 있다.
B[k][W] = B[k-1][W], if wk > W
B는 DP를 위한 최대가치를 담는 배열이고, k는 현재 넣은 물건의 번호, W은 최대 무게를 의미한다. wk 는 k번째 물건에 대한 무게를 의미한다. 따라서 위 식은 k번째 물건이 총 제한 무게를 초과한다면 k번째 최대가치를 바로 k-1번째 물건을 넣을 경우의 가치로 정하는 것이다.
만약 물건을 넣을 수 있는 무게가 조금이라도 남았다면 어떻게 해야할까? 이때 우리의 선택지는 다시 두 가지로 나뉜다.
- 새로운 물건을 넣지 않는다
- 새로운 물건을 넣기 위해 현재 물건을 넣을 공간을 만들어서 물건을 넣는다.
우리는 최대 가치를 원하기 때문에, 두 경우 중 더 큰 값을 선택하게 될 것이다. 이것을 수식으로 만들면,
B[k][W] = max(B[k-1][W], B[k][W-wk] + val(wk))
현재 물건을 넣기 위해 넣었던 물건을 뺐을 때의 가치에 현재 물건의 가치를 더해주면 된다.
문제의 적용
https://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
위 와 같은 문제를 통해서 접근해보자.
DP는 표를 만들어서 접근하면 정말 쉽다.
예제를 통해서 문제를 접근해보자.
(Wi, Vi) = (6, 13), (4, 8), (3, 6), (5, 12)
그리고 배낭이 수용 가능한 최대 무게 K = 7 이다.
맨 처음을 살펴보자 k가 0일때는 아무것도 담을 수 없다. 당연하다
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | |||||||
| 2 | 0 | |||||||
| 3 | 0 | |||||||
| 4 | 0 |
마찬가지로 k가 1,2 일때도 그렇다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | |||||
| 2 | 0 | 0 | 0 | |||||
| 3 | 0 | 0 | 0 | |||||
| 4 | 0 | 0 | 0 |
k = 3부터는 3번째 인덱스 (3, 6)로 인해 최대값을 6가질 수 있다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | ||||
| 2 | 0 | 0 | 0 | 0 | ||||
| 3 | 0 | 0 | 0 | 6 | ||||
| 4 | 0 | 0 | 0 | 6 |
k = 4부터는 (4, 8) 로 인해 최대값을 8가질 수 있다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | |||
| 2 | 0 | 0 | 0 | 0 | 8 | |||
| 3 | 0 | 0 | 0 | 6 | 8 | |||
| 4 | 0 | 0 | 0 | 6 | 8 |
k = 5부터는 (5, 12) 로 인해 최대값을 12를 가질 수 있다.
그렇다면 왜 인덱스 2,3은 8일까? (4, 8), (3, 6)로 인해서 최댓값 8을 가진다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 2 | 0 | 0 | 0 | 0 | 8 | 8 | ||
| 3 | 0 | 0 | 0 | 6 | 8 | 8 | ||
| 4 | 0 | 0 | 0 | 6 | 8 | 12 |
아래의 과정은 위와 동일하게 가져가며
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | |
| 2 | 0 | 0 | 0 | 0 | 8 | 8 | 13 | |
| 3 | 0 | 0 | 0 | 6 | 8 | 8 | 13 | |
| 4 | 0 | 0 | 0 | 6 | 8 | 12 | 13 |
결국은 k=7일때 최댓값 14을 가지게 된다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 13 |
| 2 | 0 | 0 | 0 | 0 | 8 | 8 | 13 | 13 |
| 3 | 0 | 0 | 0 | 6 | 8 | 8 | 13 | 14 |
| 4 | 0 | 0 | 0 | 6 | 8 | 12 | 13 | 14 |
이러한 원리로 점화식이 발생하며, DP에서 점화식을 찾는 것은 기본이다.
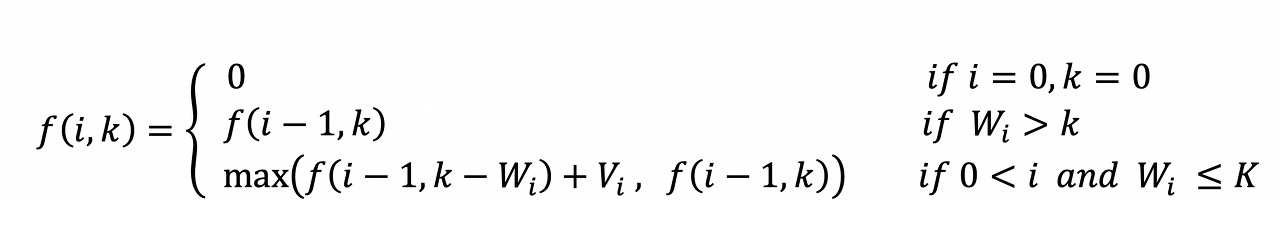
참고
https://jeonyeohun.tistory.com/86
[알고리즘 정리] 배낭 문제(Knapsack Problem)
Knapsack Problem Knapsack Problem, 배낭문제는 다이나믹 프로그래밍에서 매우 유명한 문제이다. 어떤 배낭이 있고 그 배낭안에 넣을 수 있는 최대 무게가 K라고 하자. 배낭에 넣을 수 있는 N개의 물건이
jeonyeohun.tistory.com
https://st-lab.tistory.com/141
[백준] 12865번 : 평범한 배낭 - JAVA [자바]
www.acmicpc.net/problem/12865 12865번: 평범한 배낭 첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤
st-lab.tistory.com
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] LIS, LDS (최장 증가 부분 수열, 최장 감소 부분 수열) (0) | 2023.07.31 |
|---|---|
| [Algorithm] 동적 계획법(Dynamic Programming) (0) | 2023.07.30 |
| [Algorithm] 재귀(Recursion) feat. C (0) | 2023.07.24 |
| [Algorithm] 0-1 BFS (0) | 2023.07.01 |
| [Algorithm] 내가 지금 현재 풀고 있는 알고리즘 사이트 (0) | 2023.05.04 |
배낭 문제(knapsack) 냅색 알고리즘이란
Knapsack Problem, 배낭문제는 다이나믹 프로그래밍에서 매우 유명한 문제이다.
조합 최적화(Combination Optimization) 문제 중 하나로, 주어진 공간(배낭)에 최대 가치를 가지는 물건들을 선택하는 문제이다.
일반적으로 배낭에 넣을 수 있는 총 무게(용량)가 주어지고, 물건의 무게와 해당 물건을 배낭에 넣을 때의 가치가 주어진다.
배낭 문제에는 크게 2가지의 유형이 있다.
0/1 배낭 문제(0/1 Knapscak Problem)
이 유형에서는 각 물건을 배낭에 넣을지(1) 또는 넣지 않을지(0)를 결정해야한다. 즉, 각 물건은 배낭에 한 번만 들어갈 수 있다. 이러한 제약 때문에 0/1 이라는 이름이 붙었다. 이 유형의 배낭 문제는 NP-hard문제로 알려져 있으며, 모든 가능한 조합을 시도해보려는 브루트포스(Brute-force) 방법으로는 효율적으로 해결 할 수 가 없다. 즉, DP를 사용해야한다.
분수 배낭 문제(Fractional Knapsack Problem)
이 유형에서는 각 물건을 잘게 쪼개서 일부분만 배낭에 넣을 수 있다. 즉, 물건을 부분적으로 선택할 수 있다. 이 경우 그리디(Greedy) 알고리즘이 사용될 수 있으며, 단위 무게당 가치가 높은 물건부터 차례로 넣는 방식이 최적해를 찾을 수 있다.
알고리즘 별로 유형 정리
Brute Force Approach
만약 n개의 물건이 있을 때, 가능한 모든 조합을 만들기 위해서는 2n 개의 경우의 수를 모두 시도해 보아야한다. 가지고 있는 물건이 몇개 없다면 별로 시간이 오래걸리지는 않겠지만, 2n 은 물건의 갯수가 하나만 늘어도 경우의 수가 크게 늘어나게 된다. 이 연산을 수행하려면 𝛩(2n ) 의 시간을 사용해야하고, 프로그래머 입장에서 그다지 좋은 접근은 아닐 것이다.
Dynamic Programming
따라서 이 문제는 당연스럽게도 다이나믹 프로그래밍으로 해결해야 한다. 그런데 항상 그렇듯 DP 의 가장 큰 어려움은 점화식으로 생각해야한다.
위 접근이 아닌 다른 방법으로 어떻게 접근해야 할까. 배낭에 물건을 넣을 때, 우리가 선택할 수 있는 경우는 두 가지가 있다.
- 물건을 넣는다.
- 물건을 넣지 않는다.
만약 현재 내가 넣으려고 하는 물건의 무게가 전체 제한무게를 초과한다면, 선택지는 물건을 넣지 않는 것 밖에 없다. 따라서 다음과 같은 식을 일단 하나 만들 수 있다.
B[k][W] = B[k-1][W], if wk > W
B는 DP를 위한 최대가치를 담는 배열이고, k는 현재 넣은 물건의 번호, W은 최대 무게를 의미한다. wk 는 k번째 물건에 대한 무게를 의미한다. 따라서 위 식은 k번째 물건이 총 제한 무게를 초과한다면 k번째 최대가치를 바로 k-1번째 물건을 넣을 경우의 가치로 정하는 것이다.
만약 물건을 넣을 수 있는 무게가 조금이라도 남았다면 어떻게 해야할까? 이때 우리의 선택지는 다시 두 가지로 나뉜다.
- 새로운 물건을 넣지 않는다
- 새로운 물건을 넣기 위해 현재 물건을 넣을 공간을 만들어서 물건을 넣는다.
우리는 최대 가치를 원하기 때문에, 두 경우 중 더 큰 값을 선택하게 될 것이다. 이것을 수식으로 만들면,
B[k][W] = max(B[k-1][W], B[k][W-wk] + val(wk))
현재 물건을 넣기 위해 넣었던 물건을 뺐을 때의 가치에 현재 물건의 가치를 더해주면 된다.
문제의 적용
https://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
위 와 같은 문제를 통해서 접근해보자.
DP는 표를 만들어서 접근하면 정말 쉽다.
예제를 통해서 문제를 접근해보자.
(Wi, Vi) = (6, 13), (4, 8), (3, 6), (5, 12)
그리고 배낭이 수용 가능한 최대 무게 K = 7 이다.
맨 처음을 살펴보자 k가 0일때는 아무것도 담을 수 없다. 당연하다
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | |||||||
| 2 | 0 | |||||||
| 3 | 0 | |||||||
| 4 | 0 |
마찬가지로 k가 1,2 일때도 그렇다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | |||||
| 2 | 0 | 0 | 0 | |||||
| 3 | 0 | 0 | 0 | |||||
| 4 | 0 | 0 | 0 |
k = 3부터는 3번째 인덱스 (3, 6)로 인해 최대값을 6가질 수 있다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | ||||
| 2 | 0 | 0 | 0 | 0 | ||||
| 3 | 0 | 0 | 0 | 6 | ||||
| 4 | 0 | 0 | 0 | 6 |
k = 4부터는 (4, 8) 로 인해 최대값을 8가질 수 있다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | |||
| 2 | 0 | 0 | 0 | 0 | 8 | |||
| 3 | 0 | 0 | 0 | 6 | 8 | |||
| 4 | 0 | 0 | 0 | 6 | 8 |
k = 5부터는 (5, 12) 로 인해 최대값을 12를 가질 수 있다.
그렇다면 왜 인덱스 2,3은 8일까? (4, 8), (3, 6)로 인해서 최댓값 8을 가진다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 2 | 0 | 0 | 0 | 0 | 8 | 8 | ||
| 3 | 0 | 0 | 0 | 6 | 8 | 8 | ||
| 4 | 0 | 0 | 0 | 6 | 8 | 12 |
아래의 과정은 위와 동일하게 가져가며
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | |
| 2 | 0 | 0 | 0 | 0 | 8 | 8 | 13 | |
| 3 | 0 | 0 | 0 | 6 | 8 | 8 | 13 | |
| 4 | 0 | 0 | 0 | 6 | 8 | 12 | 13 |
결국은 k=7일때 최댓값 14을 가지게 된다.
| i \ dp | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 13 | 13 |
| 2 | 0 | 0 | 0 | 0 | 8 | 8 | 13 | 13 |
| 3 | 0 | 0 | 0 | 6 | 8 | 8 | 13 | 14 |
| 4 | 0 | 0 | 0 | 6 | 8 | 12 | 13 | 14 |
이러한 원리로 점화식이 발생하며, DP에서 점화식을 찾는 것은 기본이다.
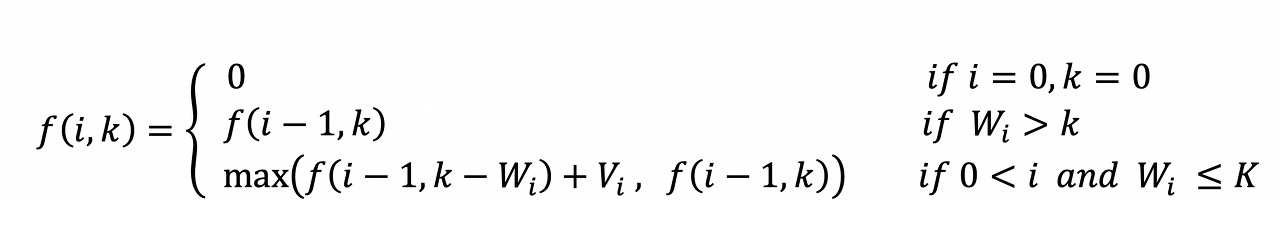
참고
https://jeonyeohun.tistory.com/86
[알고리즘 정리] 배낭 문제(Knapsack Problem)
Knapsack Problem Knapsack Problem, 배낭문제는 다이나믹 프로그래밍에서 매우 유명한 문제이다. 어떤 배낭이 있고 그 배낭안에 넣을 수 있는 최대 무게가 K라고 하자. 배낭에 넣을 수 있는 N개의 물건이
jeonyeohun.tistory.com
https://st-lab.tistory.com/141
[백준] 12865번 : 평범한 배낭 - JAVA [자바]
www.acmicpc.net/problem/12865 12865번: 평범한 배낭 첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤
st-lab.tistory.com
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] LIS, LDS (최장 증가 부분 수열, 최장 감소 부분 수열) (0) | 2023.07.31 |
|---|---|
| [Algorithm] 동적 계획법(Dynamic Programming) (0) | 2023.07.30 |
| [Algorithm] 재귀(Recursion) feat. C (0) | 2023.07.24 |
| [Algorithm] 0-1 BFS (0) | 2023.07.01 |
| [Algorithm] 내가 지금 현재 풀고 있는 알고리즘 사이트 (0) | 2023.05.04 |
