-
컴퓨터에서의 실수 표현 방식
-
고정 소수점(Fixed Point) 이란?
-
개념 및 원리
-
예제
-
장점과 단점
-
부동 소수점(Floating Point) 이란?
-
개념 및 원리
-
IEEE 754 표준
-
장점과 단점
-
고정소수점 vs 부동소수점 비교표
-
부동 소수점 오류
-
이진 표현(binary representation)의 한계
-
유한 정밀도(finite precision)의 한계
-
1. 근사 오류 (소수점 정밀도 문제)
-
2. 연산 순서에 따른 오차 누적
-
3. 대표적인 예제 (0.1 + 0.2 ≠ 0.3 문제)
-
부동 소수점 오류 해결 방법
-
1. 정수 연산을 활용한 해결 방법
-
2. 여러 언어에서의 해결책
컴퓨터에서의 실수 표현 방식
컴퓨터에서 실수를 표현하는 방식에는 두 가지가 있다.
- 고정 소수점(Fixed Point) 방식
- 부동 소수점(Floating Point) 방식
고정 소수점(Fixed Point) 이란?
고정 소수점(fixed point)은 정수를 표현하는 비트와 소수를 표현하는 비트 수를 미리 고정하여, 해당 비트만을 활용하여 실수를 표현하는 방식이다.
소수점의 위치가 고정되어 있다.
- 숫자를 저장할 때 소수점의 위치가 미리 정해져 있다.
- 예를 들어, Q8.8 형식이면 정수부 8비트 + 소수부 8비트로 고정됨.
- 즉, 모든 숫자는 항상 같은 위치에 소수점이 있다고 가정하고 저장됨.
개념 및 원리
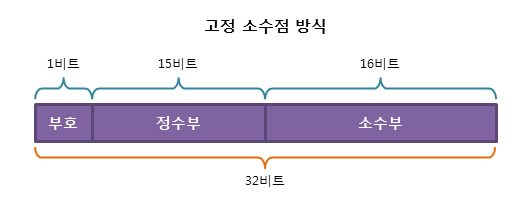
- 처음 1비트는 부호(Sign)를 나타낸다. 양수는
0, 음수는1. - 다음 15비트는 정수부(Integer Part)를 나타낸다.
- 다음 16비트는 소수부(Fractional Part)를 나타낸다.
- 정수부와 소수부의 경계를 소수점의 위치로 고정하여, 2진수로 변환된 수를 그대로 저장한다.
- 마지막으로 남는 자리는 모두
0으로 채운다.
이러한 방식으로 실수를 표현하면 특정한 범위 내에서 정밀하게 실수를 표현할 수 있으며, 하드웨어에서 효율적인 연산이 가능하다.
예제
7.625 (10) = 2² × 1 + 2¹ ×1 + 2⁰ ×1 + 2⁻¹ ×1 + 2⁻² ×0 + 2⁻³ ×1
= 111.101(2)
장점과 단점
| 장점 | 단점 |
|---|---|
| 연산이 빠르고 효율적 | 표현 가능한 범위가 제한됨 |
| 특정한 범위에서 높은 정밀도 유지 | 오버플로우 및 언더플로우 위험 |
| 일정한 비트 수로 메모리 관리 용이 | 작은 값 표현 시 부정확한 결과 발생 가능 |
부동 소수점(Floating Point) 이란?
부동 소수점(floating point) 방식은 실수를 보다 유연하고 넓은 범위에서 표현할 수 있도록 한 방식이다. 소수점의 위치가 고정되지 않고, 지수(exponent)와 가수(mantissa)의 조합을 이용해 실수를 표현한다.
소수점의 위치가 "떠다닐(floating)" 수 있다.
- 숫자를 저장할 때 소수점의 위치를 가변적으로 조정 가능.
- 지수부(exponent)와 가수부(mantissa, significand)를 이용하여 숫자의 크기에 따라 소수점의 위치를 이동함.
개념 및 원리
부동 소수점 표현 방식에서는 숫자를 아래와 같은 형태로 저장한다.
숫자 = 부호(Sign) × 가수(Mantissa) × 2^지수(Exponent)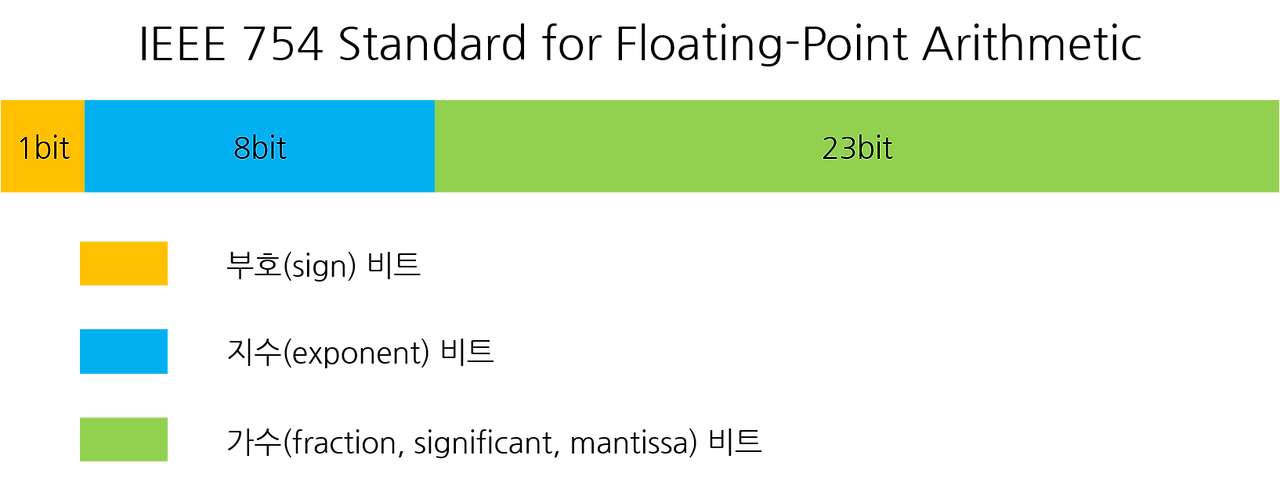
IEEE 754 표준
| 형식 | 부호(Sign) | 지수부(Exponent) | 가수부(Mantissa) |
|---|---|---|---|
| 단정밀도 (32비트) | 1비트 | 8비트 | 23비트 |
| 배정밀도 (64비트) | 1비트 | 11비트 | 52비트 |
장점과 단점
| 장점 | 단점 |
|---|---|
| 넓은 표현 범위 제공 | 특정한 10진수를 정확하게 표현 불가 |
| 동적 정밀도 지원 | 연산 시 오차 발생 가능 |
| 다양한 수를 다룰 때 연산의 유연성 제공 | 연산 비용이 높아 성능 저하 가능 |
고정소수점 vs 부동소수점 비교표
| 특징 | 고정소수점 (Fixed-Point) | 부동소수점 (Floating-Point) |
| 정확성 | 특정 범위 내에서는 정밀도 유지 | 넓은 범위를 표현 가능하지만 근사값 저장 |
| 연산 속도 | 빠름 (정수 연산 기반) | 느림 (복잡한 연산 필요) |
| 메모리 사용 | 작음 (일반적으로 16비트 또는 32비트) | 큼 (일반적으로 32비트 또는 64비트) |
| 표현 가능한 범위 | 제한적 (고정된 크기) | 넓음 (지수부 덕분에 큰 수 표현 가능) |
| 정밀도 문제 | 특정 소수를 정확히 표현하지 못함 | 일부 소수를 근사값으로 저장 |
부동 소수점 오류
컴퓨터에서 부동소수점(Floating Point) 오류가 발생하는 주된 이유는 이진 표현(binary representation)과 유한 정밀도(finite precision)의 한계 때문이다.
이진표현과 유한정밀도의 한계??? 무엇일까?
이진 표현(binary representation)의 한계
컴퓨터는 모든 숫자를 2진수(0과 1)로 저장한다.
그런데, 우리가 10진수에서 쉽게 표현할 수 있는 일부 소수(예: 0.1, 0.2)는 2진수로 변환하면 무한히 반복되는 형태가 된다.
0.1을 10진수로 쓰면:
0.1 (10진수)하지만, 이를 2진수로 변환하면:
0.00011001100110011001100110011...(2진수, 무한 반복)
즉, 0.1은 2진법에서는 끝없이 반복되는 숫자이기 때문에, 컴퓨터는 유한한 비트 수를 사용해 이를 "잘라서" 저장해야 한다.
이 과정에서 근사값(approximation)으로 저장하게 되고, 작은 오차가 발생한다.
결과적으로, 일부 소수는 컴퓨터가 정확하게 표현할 수 없다.
사람이 0.1이라고 입력했지만, 실제로 저장된 값은 0.09999999999999999처럼 미세한 차이가 있을 수 있다.
유한 정밀도(finite precision)의 한계
컴퓨터는 무한한 숫자를 저장할 수 없고, 정해진 크기의 메모리(비트 수) 안에서 숫자를 표현해야 한다.
즉, 부동소수점 숫자는 정밀도가 제한되어 있으며, 일정한 크기까지만 저장할 수 있다.
예를 들어, IEEE 754 표준에서는:
- 32비트(단정밀도): 약 7자리까지만 정확하게 표현 가능
- 64비트(배정밀도): 약 15~16자리까지만 정확하게 표현 가능
즉, 0.1을 저장할 때 64비트 안에서 표현할 수 있는 가장 가까운 근사값을 저장하지만, 완벽히 0.1이 아님!
print(0.1 + 0.2) # 출력: 0.30000000000000004사람이 보기에는 0.1 + 0.2 = 0.3이어야 하지만, 컴퓨터가 0.1과 0.2를 정확히 저장할 수 없기 때문에, 계산 결과가 0.30000000000000004처럼 미세한 오류가 발생한다.
고정 소수점에서는 문제가 발생하지 않는걸까? -> 발생한다. 하지만 고정 소수점에서는 소수부 비트 제한으로 인해 특정 숫자가 반올림 되어 문제가 크게 부각되지 않는다.
1. 근사 오류 (소수점 정밀도 문제)
부동 소수점 연산은 무한소수를 정확하게 표현하지 못하기 때문에 오차가 발생할 수 있다.
public class Main {
public static void main(String[] args) {
double a = 0.1;
double b = 0.2;
double sum = a + b;
System.out.println(sum); // 출력: 0.30000000000000004
}
}
2. 연산 순서에 따른 오차 누적
public class Main {
public static void main(String[] args) {
double x = 1.0;
double y = 1e-16;
System.out.println((x + y) - x); // 1e-16이 아니라 0이 나올 수 있음
}
}
3. 대표적인 예제 (0.1 + 0.2 ≠ 0.3 문제)
0.1(10) → 0.0001100110011001100110011001100...(2)
0.2(10) → 0.0011001100110011001100110011001...(2)
0.3(10) → 0.0100110011001100110011001100110...(2)
부동 소수점 오류 해결 방법
1. 정수 연산을 활용한 해결 방법
public class Main {
public static void main(String[] args) {
int a = 10;
int b = 20;
int sum = a + b;
System.out.println(sum / 10.0); // 0.3 정확하게 출력
}
}
2. 여러 언어에서의 해결책
Python
from decimal import Decimal
a = Decimal('0.1')
b = Decimal('0.2')
print(a + b) # 정확히 0.3 출력
C++ (GMP 라이브러리 활용)
#include <iostream>
#include <gmpxx.h>
int main() {
mpf_class a("0.1"), b("0.2");
mpf_class sum = a + b;
std::cout << sum << std::endl; // 정확히 0.3 출력
return 0;
}
Java (BigDecimal 활용)
import java.math.BigDecimal;
public class Main {
public static void main(String[] args) {
BigDecimal a = new BigDecimal("0.1");
BigDecimal b = new BigDecimal("0.2");
System.out.println(a.add(b)); // 정확히 0.3 출력
}
}
JavaScript (Big.js 활용)
const Big = require('big.js');
let a = new Big('0.1');
let b = new Big('0.2');
console.log(a.plus(b).toString()); // 정확히 0.3 출력
이러한 방법들을 활용하면 부동 소수점 연산에서 발생하는 오류를 효과적으로 줄일 수 있다.
'Computer Science' 카테고리의 다른 글
| [CS] JPG 와 PNG에 대해서 알아보자. (0) | 2024.06.13 |
|---|---|
| [CS] 부동 소수점 오류 (0) | 2024.06.01 |
컴퓨터에서의 실수 표현 방식
컴퓨터에서 실수를 표현하는 방식에는 두 가지가 있다.
- 고정 소수점(Fixed Point) 방식
- 부동 소수점(Floating Point) 방식
고정 소수점(Fixed Point) 이란?
고정 소수점(fixed point)은 정수를 표현하는 비트와 소수를 표현하는 비트 수를 미리 고정하여, 해당 비트만을 활용하여 실수를 표현하는 방식이다.
소수점의 위치가 고정되어 있다.
- 숫자를 저장할 때 소수점의 위치가 미리 정해져 있다.
- 예를 들어, Q8.8 형식이면 정수부 8비트 + 소수부 8비트로 고정됨.
- 즉, 모든 숫자는 항상 같은 위치에 소수점이 있다고 가정하고 저장됨.
개념 및 원리
- 처음 1비트는 부호(Sign)를 나타낸다. 양수는
0, 음수는1. - 다음 15비트는 정수부(Integer Part)를 나타낸다.
- 다음 16비트는 소수부(Fractional Part)를 나타낸다.
- 정수부와 소수부의 경계를 소수점의 위치로 고정하여, 2진수로 변환된 수를 그대로 저장한다.
- 마지막으로 남는 자리는 모두
0으로 채운다.
이러한 방식으로 실수를 표현하면 특정한 범위 내에서 정밀하게 실수를 표현할 수 있으며, 하드웨어에서 효율적인 연산이 가능하다.

예제
7.625 (10) = 2² × 1 + 2¹ ×1 + 2⁰ ×1 + 2⁻¹ ×1 + 2⁻² ×0 + 2⁻³ ×1
= 111.101(2)
장점과 단점
| 장점 | 단점 |
|---|---|
| 연산이 빠르고 효율적 | 표현 가능한 범위가 제한됨 |
| 특정한 범위에서 높은 정밀도 유지 | 오버플로우 및 언더플로우 위험 |
| 일정한 비트 수로 메모리 관리 용이 | 작은 값 표현 시 부정확한 결과 발생 가능 |
부동 소수점(Floating Point) 이란?
부동 소수점(floating point) 방식은 실수를 보다 유연하고 넓은 범위에서 표현할 수 있도록 한 방식이다. 소수점의 위치가 고정되지 않고, 지수(exponent)와 가수(mantissa)의 조합을 이용해 실수를 표현한다.
소수점의 위치가 "떠다닐(floating)" 수 있다.
- 숫자를 저장할 때 소수점의 위치를 가변적으로 조정 가능.
- 지수부(exponent)와 가수부(mantissa, significand)를 이용하여 숫자의 크기에 따라 소수점의 위치를 이동함.
개념 및 원리
부동 소수점 표현 방식에서는 숫자를 아래와 같은 형태로 저장한다.
숫자 = 부호(Sign) × 가수(Mantissa) × 2^지수(Exponent)
IEEE 754 표준
| 형식 | 부호(Sign) | 지수부(Exponent) | 가수부(Mantissa) |
|---|---|---|---|
| 단정밀도 (32비트) | 1비트 | 8비트 | 23비트 |
| 배정밀도 (64비트) | 1비트 | 11비트 | 52비트 |
장점과 단점
| 장점 | 단점 |
|---|---|
| 넓은 표현 범위 제공 | 특정한 10진수를 정확하게 표현 불가 |
| 동적 정밀도 지원 | 연산 시 오차 발생 가능 |
| 다양한 수를 다룰 때 연산의 유연성 제공 | 연산 비용이 높아 성능 저하 가능 |
고정소수점 vs 부동소수점 비교표
| 특징 | 고정소수점 (Fixed-Point) | 부동소수점 (Floating-Point) |
| 정확성 | 특정 범위 내에서는 정밀도 유지 | 넓은 범위를 표현 가능하지만 근사값 저장 |
| 연산 속도 | 빠름 (정수 연산 기반) | 느림 (복잡한 연산 필요) |
| 메모리 사용 | 작음 (일반적으로 16비트 또는 32비트) | 큼 (일반적으로 32비트 또는 64비트) |
| 표현 가능한 범위 | 제한적 (고정된 크기) | 넓음 (지수부 덕분에 큰 수 표현 가능) |
| 정밀도 문제 | 특정 소수를 정확히 표현하지 못함 | 일부 소수를 근사값으로 저장 |
부동 소수점 오류
컴퓨터에서 부동소수점(Floating Point) 오류가 발생하는 주된 이유는 이진 표현(binary representation)과 유한 정밀도(finite precision)의 한계 때문이다.
이진표현과 유한정밀도의 한계??? 무엇일까?
이진 표현(binary representation)의 한계
컴퓨터는 모든 숫자를 2진수(0과 1)로 저장한다.
그런데, 우리가 10진수에서 쉽게 표현할 수 있는 일부 소수(예: 0.1, 0.2)는 2진수로 변환하면 무한히 반복되는 형태가 된다.
0.1을 10진수로 쓰면:
0.1 (10진수)하지만, 이를 2진수로 변환하면:
0.00011001100110011001100110011...(2진수, 무한 반복)
즉, 0.1은 2진법에서는 끝없이 반복되는 숫자이기 때문에, 컴퓨터는 유한한 비트 수를 사용해 이를 "잘라서" 저장해야 한다.
이 과정에서 근사값(approximation)으로 저장하게 되고, 작은 오차가 발생한다.
결과적으로, 일부 소수는 컴퓨터가 정확하게 표현할 수 없다.
사람이 0.1이라고 입력했지만, 실제로 저장된 값은 0.09999999999999999처럼 미세한 차이가 있을 수 있다.
유한 정밀도(finite precision)의 한계
컴퓨터는 무한한 숫자를 저장할 수 없고, 정해진 크기의 메모리(비트 수) 안에서 숫자를 표현해야 한다.
즉, 부동소수점 숫자는 정밀도가 제한되어 있으며, 일정한 크기까지만 저장할 수 있다.
예를 들어, IEEE 754 표준에서는:
- 32비트(단정밀도): 약 7자리까지만 정확하게 표현 가능
- 64비트(배정밀도): 약 15~16자리까지만 정확하게 표현 가능
즉, 0.1을 저장할 때 64비트 안에서 표현할 수 있는 가장 가까운 근사값을 저장하지만, 완벽히 0.1이 아님!
print(0.1 + 0.2) # 출력: 0.30000000000000004사람이 보기에는 0.1 + 0.2 = 0.3이어야 하지만, 컴퓨터가 0.1과 0.2를 정확히 저장할 수 없기 때문에, 계산 결과가 0.30000000000000004처럼 미세한 오류가 발생한다.
고정 소수점에서는 문제가 발생하지 않는걸까? -> 발생한다. 하지만 고정 소수점에서는 소수부 비트 제한으로 인해 특정 숫자가 반올림 되어 문제가 크게 부각되지 않는다.
1. 근사 오류 (소수점 정밀도 문제)
부동 소수점 연산은 무한소수를 정확하게 표현하지 못하기 때문에 오차가 발생할 수 있다.
public class Main {
public static void main(String[] args) {
double a = 0.1;
double b = 0.2;
double sum = a + b;
System.out.println(sum); // 출력: 0.30000000000000004
}
}
2. 연산 순서에 따른 오차 누적
public class Main {
public static void main(String[] args) {
double x = 1.0;
double y = 1e-16;
System.out.println((x + y) - x); // 1e-16이 아니라 0이 나올 수 있음
}
}
3. 대표적인 예제 (0.1 + 0.2 ≠ 0.3 문제)
0.1(10) → 0.0001100110011001100110011001100...(2)
0.2(10) → 0.0011001100110011001100110011001...(2)
0.3(10) → 0.0100110011001100110011001100110...(2)
부동 소수점 오류 해결 방법
1. 정수 연산을 활용한 해결 방법
public class Main {
public static void main(String[] args) {
int a = 10;
int b = 20;
int sum = a + b;
System.out.println(sum / 10.0); // 0.3 정확하게 출력
}
}
2. 여러 언어에서의 해결책
Python
from decimal import Decimal
a = Decimal('0.1')
b = Decimal('0.2')
print(a + b) # 정확히 0.3 출력
C++ (GMP 라이브러리 활용)
#include <iostream>
#include <gmpxx.h>
int main() {
mpf_class a("0.1"), b("0.2");
mpf_class sum = a + b;
std::cout << sum << std::endl; // 정확히 0.3 출력
return 0;
}
Java (BigDecimal 활용)
import java.math.BigDecimal;
public class Main {
public static void main(String[] args) {
BigDecimal a = new BigDecimal("0.1");
BigDecimal b = new BigDecimal("0.2");
System.out.println(a.add(b)); // 정확히 0.3 출력
}
}
JavaScript (Big.js 활용)
const Big = require('big.js');
let a = new Big('0.1');
let b = new Big('0.2');
console.log(a.plus(b).toString()); // 정확히 0.3 출력
이러한 방법들을 활용하면 부동 소수점 연산에서 발생하는 오류를 효과적으로 줄일 수 있다.
'Computer Science' 카테고리의 다른 글
| [CS] JPG 와 PNG에 대해서 알아보자. (0) | 2024.06.13 |
|---|---|
| [CS] 부동 소수점 오류 (0) | 2024.06.01 |
