시간 복잡도란?
시간 복잡도(Time Complexity)는 알고리즘의 절대적인 실행 시간을 나타내는 것이 아닌 알고리즘을 수행하는 데 연산들이 몇 번 이루어지는 지를 숫자로 표기한다.
알고리즘의 성능 평가 Case
- 최선의 경우 (Best Case)
최적의 입력을 한 상태에서, 작업을 완료하는 데 가장 연산 횟수가 적은 경우 - 최악의 경우 (Worst Case)
최악의 입력을 한 상태에서, 작업을 완료하는 데 가장 연산 횟수가 많은 경우 - 평균의 경우 (Average Case)
여러 경우의 수를 고려하여, 총 연산 횟수를 계산하고 시행 횟수로 나눈 경우
알고리즘 분석 시 평균의 경우와 최악의 경우가 가장 많이 활용되며, 알고리즘이 복잡해질수록 평균을 구하기 어려워져 최악의 경우로 알고리즘 성능을 파악한다.
공간 복잡도란?
공간 복잡도(Space Complexity)란, 프로그램을 실행시킨 후 완료하는 데 필요로 하는 자원 공간의 양을 말한다.
- 알고리즘과 무관한 공간, 즉 고정 공간
- 코드가 저장되는 공간, 알고리즘 실행을 위해 시스템이 필요로 하는 공간 등
- 알고리즘과 밀접한 공간, 즉 가변 공간
- 문제를 해결하기 위해 알고리즘이 필요로 하는 공간. 변수를 저장하는 공간, 순환 프로그램일 경우 순환 스택(recursion stack) 등
그렇다면 복잡도는 왜 중요할까?
시대가 흐름에 따라 과거에 비해서 프로그램의 규모는 시간이 지날수록 방대해지고 있다. 즉, 처리해야하는 데이터의 양이 많아진다는 것이다. 입력하는 데이터의 양이 적은 경우에는 무시해도 크게 상관이 없을 수 있지만 그 양이 많아지면 알고리즘 간의 효율성 차이는 커질 수 밖에 없기 때문이다.
그렇기에 개발자들은 더 효율적인 알고리즘을 고려해야한다. (기업에서 코테를 보는 이유)
빅오(Big-O) 표기법
엄밀한 정의는 아니지만, 빅오 표기법을 간단하게 정의하자면 가장 빠르게 증가하는 항만을 고려하는 표기법이다.
연산 횟수가 다항식으로 표현될 경우, 최고차항을 제외한 모든 항과 최고차항의 계수를 제외시켜 나타낸다.


빅오의 순서는 위와 같으며, 커질 수록 연산 횟수가 더 많다고 연산에 더 오랜시간이 걸린다는 뜻이다.
O(1) - 상수 시간(Constant time)
입력 크기에 상관없이 일정한 연산을 수행하면 시간복잡도는 O(1)이다.
void func (int n) {
printf("%d\n", n);
}O(logN) - 로그 시간 (Logarithmic time)
입력 크기(N)가 커질 때 연산횟수가 logN에 비례해서 증가하면서 시간 복잡도는 O(logN)이다.
for(i=1; i<=n; i*2) {
...
}
O(N) - 선형 시간(Linear time)
입력 크기(N)가 커질 때 연산 횟수가 N에 비례해서 증가하면 시간 복잡도는 O(N)이다.
for(i=0; i < n; i++) {
...
}
O(N^2) - 2차 시간(Quadratic time)
입력 크기(N)가 커질 때 연산횟수가 N^2에 비례해서 증가하면 시간 복잡도는 O(N^2)이다.
for(i=0; i < n; i++) {
for(j=0, j < n; j++) {
...
}
}
O(2^N) - 지수 시간(Exponential time)
입력 크기가 커질 때 연산수가 2^N에 비례해서 증가하면 시간복잡도는 O(2^N)이다.
int func (int n) {
if (n <= 1)
return n;
return func(n-1) + fun(n-2);
}
표 정리
| 복잡도 | 소요 시간 | 예시 |
| O(1) | 상수 시간 | 스택에서 Push, Pop |
| O(log n) | 로그 시간 | 이진 트리 |
| O(n) | 직선적 시간 | for 문 |
| O(n log n) | 선형 로그 시간 | 퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap sort) |
| O(n^2) | 2차 시간 | 이중 for 문, 삽입 정렬(insertion sort), 거품 정렬(bubble sort), 선택 정렬(selection sort) |
| O(C^n) | 지수 시간 | 피보나치 수열 |
공간복잡도 또한 위와 비슷하게 빅오표기법으로 나타낼 수 있다.
int sum(int a[], int n)
{
int x = 0;
for(int i = 0; i < n; i++) {
x = x + a[i];
}
return(x);
}위 알고리즘은 4개의 변수를 사용하고 있다.
- int arr[n] : 4*n byte (입력 공간)
- int n : 4 byte (입력 공간)
- int x : 4 byte (보조 공간)
- int i : 4 byte (보조 공간)
총 4n+12 에 메모리를 요구한다.
메모리가 입력 값에 따라 선형적으로 증가하기 때문에 공간 복잡도는 O(n)이 된다.
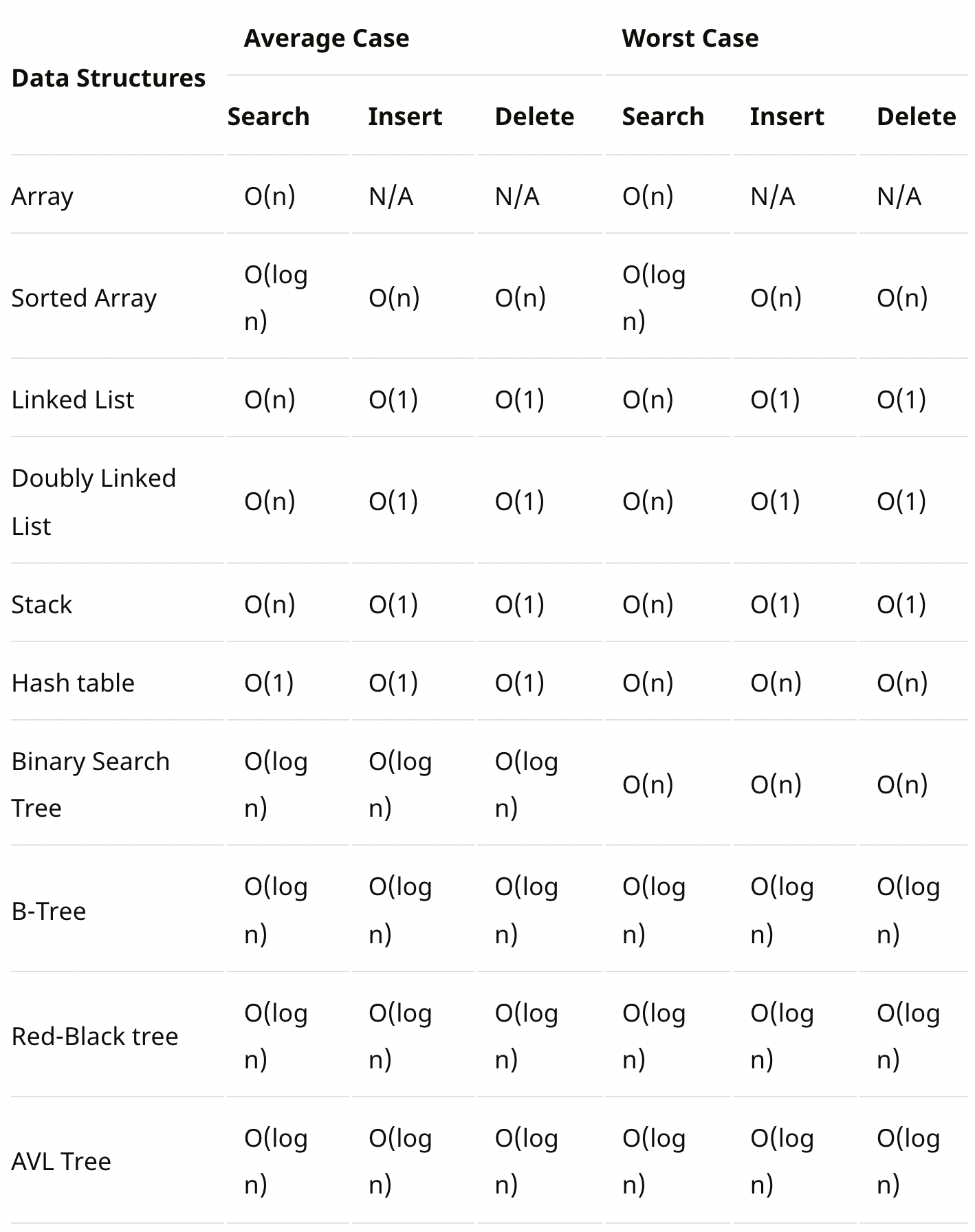
자료구조별 시간 복잡도
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm] 유니온 파인드(Union-Find) 알고리즘 (0) | 2023.04.21 |
|---|---|
| [Algorithm] 플로이드 와샬(Floyd Warshall) 알고리즘 (0) | 2023.04.14 |
| [Algorithm] 그리디 알고리즘 (Greedy) (2) | 2023.04.06 |
| [Algorithm] 브루트포스 알고리즘 (BruteForce) (0) | 2023.03.21 |
| [Algorithm] Hash(해시) 란 (0) | 2023.03.18 |
